그래프 - Graph란 요소들이 서로 복잡하게 연결되어 있는 관계를 표현하는 자료구조이다.

용어 정리

정점 - vertex

노드 - node라고하며 데이터가 저장되는 그래프의 기본 원소이다.

간선 - edge

링크 - link라고하며 정점 간의 관계를 나타낸다

인접 정점 - adjacent vertex

하나의 정점에서 간선에 의해 직접 연결되어 있는 정점을 뜻한다.

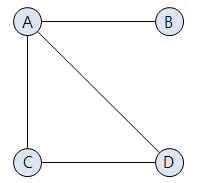
위 그래프에서 정점 C의 인접 정점은 A, D이다.

차수 - degree

정점에 연결된 간선의 수

정점 A의 차수는 3이고 모든 정점의 차수를 합하면 8이다.

  • 무방향 그래프에서 하나의 간선은 두 개의 정점에 인접하기 때문에 간선 수에 2배를 해주면 된다.
  • 방향 그래프의 경우 외부에서 오는 간선의 수를 진입 차수 - in-degree라고 하며,
  • 외부로 향하는 간선의 수를 진출 차수 - out-degree라고 한다.

경로 - path

간선을 따라갈 수 있는 길을 말하며, 정점을 나열하여 표시한다.

경로의 길이 - length

경로를 구성하는 데 사용된 간선의 수를 뜻한다.

단순 경로 - simple path

경로 중 반복되는 간선이 없는 경로

사이클 - cycle

시작 정점과 종료 정점이 같은 단순 경로를 뜻한다.

그래프 ADT

객체

정점의 집합과 건선의 집합

연산

  • create() : 그래프 생성
  • insertVertex(v) : 그래프에 정점 v 삽입
  • insertEdge(u, v) : 그래프에 u정점과 v정점을 연결하는 간선 삽입
  • deleteVertex(v) : 그래프에서 정점 v 삭제 (v에 연결된 모든 간선도 함께 삭제)
  • deleteEdge(u, v) : 그래프에서 u정점과 v정점을 연결하는 간선 삭제
  • adjacent(v) : 정점 v에 인접한 모든 정점을 반환

구현 방법

인접 행렬, 인접 리스트 로 구현할 수 있다.

1. 인접 행렬 - Adjacency Materix

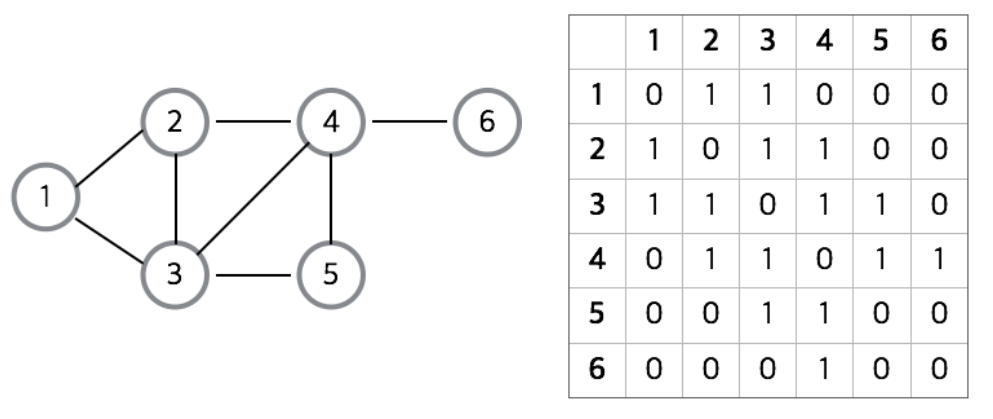
장점

  • 두 점에 대한 연결 정보를 조회할 때 O(1)시간복잡도를 가진다.

    2차원 배열 속 모든 정점들의 간선 정보를 담는다.

  • 정점(i)의 차수를 구할 때는 다음과 같이 인접행렬(M)의 i번째 행의 값을 모두 더하면 되므로 O(n)의 시간복잡도를 가진다.
    \(degree(i)= \sum_{k=0}^{n-1} M[i][k]\)

  • 구현이 비교적 간단하다.

단점

  • 모든 간선의 수를 알아내려면 모든 정점에 대해 간선 정보를 대입해야 하므로 O(n²)의 시간복잡도를 가진다.
  • 무조건 2차원 배열이 필요하여 필요 이상의 공간이 낭비된다.

2. 인접 리스트

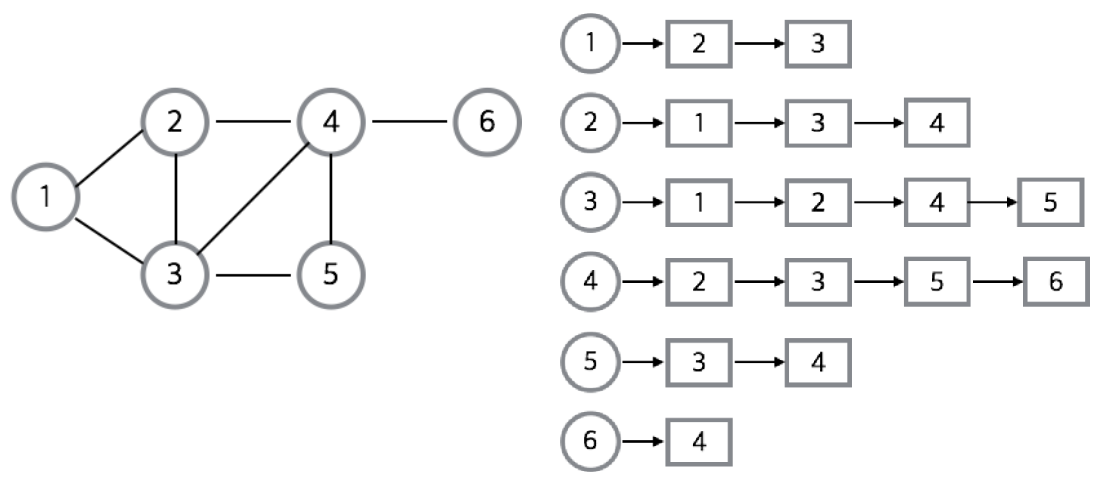
장점

  • 정점들의 연결 정보를 탐색할 때 O(n)의 시간복잡도를 가진다. n = 간선의 갯수
  • 필요한 만큼의 공간만 사용하기 때문에 공간의 낭비가 적다.

단점

  • 두 정점을 연결하는 간선을 조회하거나 정점의 차수를 알기 위해서는 정점의 인접 리스트를 탐색해야 하므로 정점의 차수만큼의 시간이 필요하다. O(degree(v)) v = 정점

  • 구현이 비교적 어렵다.

3. 인접 행렬 vs 인접 리스트

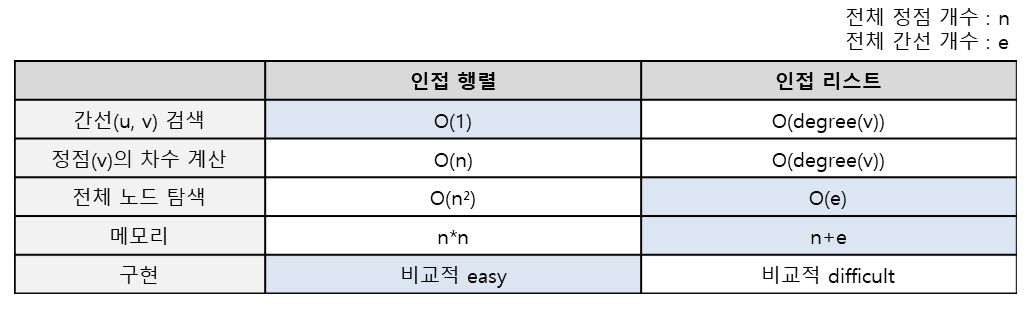
  • 정점의 개수에 비해 간선의 개수가 매우 적은 희소 그래프에서는 인접 리스트가 유리할 수 있다.
  • 모든 정점간에 간선이 존재하는 완전그래프 에서는 인접 행렬이 유리할 수 있다.

다음글 트리 - tree

Reference

  • https://suyeon96.tistory.com/32#—%–%EA%B-%B-%EB%-E%–%ED%–%–%–%EC%-A%A-%EC%–%B-
  • https://coding-factory.tistory.com/610